Raytracing – lokálne osvetľovacie modely
Raytracing – lokálne osvetľovacie modely
10. mája 2014 Žiadne komentáre na Raytracing – lokálne osvetľovacie modelyRendering equation (renderovacia rovnica)
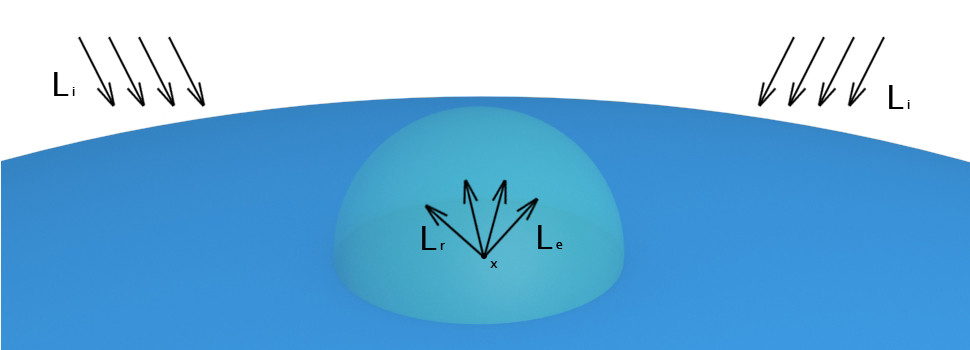
Predstavme si lokálnu situáciu osvetľovania všeobecne. V každom bode scény X=(x,y,z) dochádza k istým zmenám osvetlenia. Tento bod môže nejaké svetlo sám vyžarovať do rôznych smerov, a takisto do tohto bodu X môže nejaká svetelná energia prichádzať, z rôznych smerov z rôznych zdrojov a v danom bode sa môže rôzne meniť na základe vlastností daného bodu. Úplne všeobecná funkcia pre vyjadrenie energie vychádzajúcej z tohto bodu by bola integrálna funkcia obsahujúca nespojité podintegrálne funkcie a nevedeli by sme ju numericky riešiť. Preto používame numerické aproximácie, teda raytracing.
Energiu vychádzajúcu z bodu nazveme radiancia (radiance) a bude označovať funkciu 5 premenných, kde prvé tri budú pozícia x,y,z daného bodu a dve budú pre smer (sférické súradnice). Máme teda:
![]() Ako sme už spomenuli, daný bod môže energiu odrážať aj emitovať. Tieto dve veličiny sú nezávislé, teda výsledná vyžarujúca energia bude ich súčet. Označme emitujúcu energiu ako Le, odrazenú energiu ako Lr, dostaneme:
Ako sme už spomenuli, daný bod môže energiu odrážať aj emitovať. Tieto dve veličiny sú nezávislé, teda výsledná vyžarujúca energia bude ich súčet. Označme emitujúcu energiu ako Le, odrazenú energiu ako Lr, dostaneme:
![]() Emitujúca energia je daná priamo vlastnosťami daného svetelného zdroja. Ak daný bod nie je svetelným zdrojom, hodnota Le bude nulová. Avšak odrazená energia závisí od vlastností povrchového materiálu, preto sa na Lr časť funkcie pozrieme bližšie. Do bodu x isté žiarenie prichádza, označme ho nasledovne, kde omega s čiarkou je smer, z ktorého žiarenie prichádza:
Emitujúca energia je daná priamo vlastnosťami daného svetelného zdroja. Ak daný bod nie je svetelným zdrojom, hodnota Le bude nulová. Avšak odrazená energia závisí od vlastností povrchového materiálu, preto sa na Lr časť funkcie pozrieme bližšie. Do bodu x isté žiarenie prichádza, označme ho nasledovne, kde omega s čiarkou je smer, z ktorého žiarenie prichádza:
![]() Toto prichádzajúce žiarenie bude modifikované aj v závislosti uhlu, pod ktorým na povrch dopadá. Vo výpočte teda použijeme aj normálu n povrchu v danom bode x. Funkcia fr je funkcia kontribúcie daného prichádzajúceho žiarenia na základe vlastností povrchu. Teda pre jeden prichádzajúci smer omega s čiarkou dostávame nasledujúci výraz pre odchádzajúcu energiu.
Toto prichádzajúce žiarenie bude modifikované aj v závislosti uhlu, pod ktorým na povrch dopadá. Vo výpočte teda použijeme aj normálu n povrchu v danom bode x. Funkcia fr je funkcia kontribúcie daného prichádzajúceho žiarenia na základe vlastností povrchu. Teda pre jeden prichádzajúci smer omega s čiarkou dostávame nasledujúci výraz pre odchádzajúcu energiu.
![]()
Avšak žiarenie môže prichádzať z úplne všetkých smerov okolo bodu x. Výsledné odchádzajúce žiarenie teda musíme rátať ako integrál cez tento priestor (zvyčajne cez pologuľu, pokiaľ ide o bod na ploche).
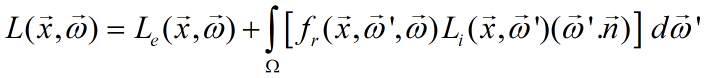 A toto je teda všeobecná renderovacia rovnica pre bod x v priestore. Ako vyjadríme funkciu fr, na to sa pozrieme v nasledujúcej časti tohto článku.
A toto je teda všeobecná renderovacia rovnica pre bod x v priestore. Ako vyjadríme funkciu fr, na to sa pozrieme v nasledujúcej časti tohto článku.
BRDF – Bidirectional Reflectance Distribution Function (dvojsmerná odrazivá distribučná funkcia)
BRDF slúži na popísanie odrazu svetla od daného povrchu. Predpokladá, že svetlo sa odráža na tom istom mieste povrchu, do ktorého naň narazilo. Závisí od smeru príchodu svetla a smeru odrazu svetla. Je teda 7 rozmerná, 3 rozmery pre pozíciu a dva pre každý smer odrazu. Funkciu vyjadríme nasledovne:
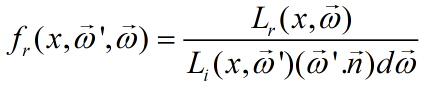 kde menovateľ na pravej strane je súčin prichádzajúcej svetelnej energie, uhol natočenia danej plochy ku svetlu a priestorového uhla. BRDF spĺňa Helmholtzove pravidlo reciprocity, to znamená, že sa nič nezmení pri výmene svetla a kamery, jednoducho povedané ak sa pozeráme sprava a svetlo svieti zľava, je to to isté ako keby sme sa pozerali zľava a svetlo by svietilo sprava. Platí to však iba pre izotropické materiály, tj. také, ktoré majú rovnaké vlastnosti povrchu nezávisle od smeru pohľadu na povrch. BRDF zachováva energiu. Od povrchu sa nemôže odraziť viac svetla, ako sa prijalo.
kde menovateľ na pravej strane je súčin prichádzajúcej svetelnej energie, uhol natočenia danej plochy ku svetlu a priestorového uhla. BRDF spĺňa Helmholtzove pravidlo reciprocity, to znamená, že sa nič nezmení pri výmene svetla a kamery, jednoducho povedané ak sa pozeráme sprava a svetlo svieti zľava, je to to isté ako keby sme sa pozerali zľava a svetlo by svietilo sprava. Platí to však iba pre izotropické materiály, tj. také, ktoré majú rovnaké vlastnosti povrchu nezávisle od smeru pohľadu na povrch. BRDF zachováva energiu. Od povrchu sa nemôže odraziť viac svetla, ako sa prijalo.
Viac o BRDF sa dočítate aj na wikipédii.
Diffuse Reflection (difúzny odraz)
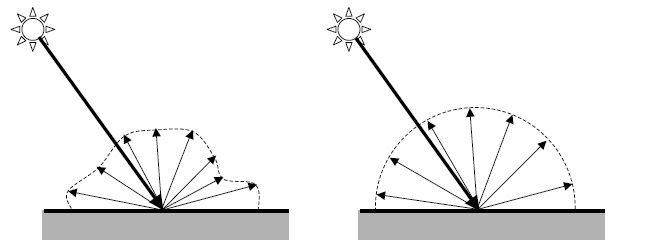
Difúzny odraz je taký, ktorý odráža prichádzajúce svetlo do všetkých smerov, nezávisle od toho, z ktorého smeru svetlo prišlo. Ak sa svetlo odráža do všetkých smerov s úplne rovnakou distribúciou, nazýva sa Lambertian diffuse reflection, na obrázku nižšie vpravo. Pri obyčajnom difúznom odraze (obrázok nižšie vľavo) platí, čím je väčší uhol medzi normálou plochy a vektorom prichádzajúceho svetla, tým vznikne väčší lesk. Pre odrazenú difúznu zložku svetla teda platí nasledujúci vzorec:
![]() kde Il je prichádzajúca intenzita svetla, kd je konštanta určujúca koľko svetla sa odrazí (a koľko pohltí), l je vektor prichádzajúceho svetla a n je normála plochy.
kde Il je prichádzajúca intenzita svetla, kd je konštanta určujúca koľko svetla sa odrazí (a koľko pohltí), l je vektor prichádzajúceho svetla a n je normála plochy.
Specular Reflection (zrkadlový odraz)
Tento odraz simuluje vlastnosti skleneného alebo zrkadlového povrchu. V ideálnom prípade (zrkadlo) odráža lúč priamo (uhol odrazu=uhol dopadu, podľa normály). V neideálnom prípade sa svetlo odráža v smeroch v akomsi tvare kužeľa okolo priameho uhla odrazu. Vytvára to lesk, podobne ako pri difúznom odraze, ale oveľa viac sústredený odlesk, práve v oblasti toho kužeľa.
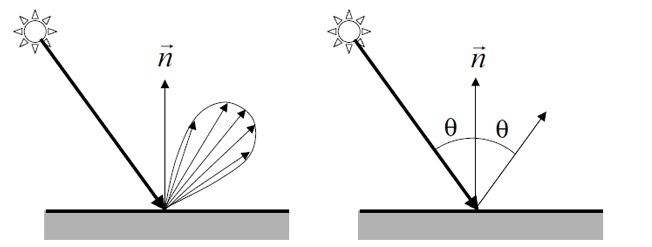
Tento zrkadlový odraz má rovnicu:
![]() Zrkadlový odraz môžeme popísať aj pomocou BRDF pomocou sférických súradníc, a to nasledovne:
Zrkadlový odraz môžeme popísať aj pomocou BRDF pomocou sférických súradníc, a to nasledovne:
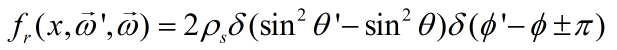 kde ró s je konštanta popisujúca spekulárny lesk. Výsledkom je funkcia, ktorá bude nenulová, iba ak sa theta bude rovnať theta s čiarkou, čiže v prípade zrkadlového lesku.
kde ró s je konštanta popisujúca spekulárny lesk. Výsledkom je funkcia, ktorá bude nenulová, iba ak sa theta bude rovnať theta s čiarkou, čiže v prípade zrkadlového lesku.
Fresnel Reflection (Fresnelov odraz/lesk)
Fresnelov odraz popisuje odraz svetla, ktorý závisí aj od vlnovej dĺžky prichádzajúceho svetla. Väčšinou ho pozorujeme pod ostrými uhlami (85 stupňov a viac). Odrazené žiarenie má nasledovný vzťah:
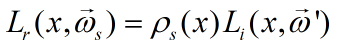 kde konštantu ró s môžeme s Fresnelov vyjadriť ako:
kde konštantu ró s môžeme s Fresnelov vyjadriť ako:
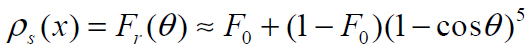 Bude závisieť aj od uhlu, teda pod každým uhlom sa odrazí mierne iná intenzita svetla.
Bude závisieť aj od uhlu, teda pod každým uhlom sa odrazí mierne iná intenzita svetla.
Refraction (lom svetla)
Objekty v scéne majú často transparentný/priesvitný materiál. To znamená, že lúč prichádzajúci na tento povrch sa láme aj dovnútra materiálu. Aby sme docielili čím väčšiu podobnosť reálnemu svetu, tento lúč sa musí lámať na základe lomu svetla pre daný materiál. Využijeme Snellov zákon o lome svetla z fyziky, ktorý má nasledujúci tvar:
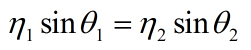 kde eta 1 a eta 2 sú indexi lomu daných dvoch prostredí, a uhly sú uhly daných lúčov, ako vidieť aj na obrázku:
kde eta 1 a eta 2 sú indexi lomu daných dvoch prostredí, a uhly sú uhly daných lúčov, ako vidieť aj na obrázku:
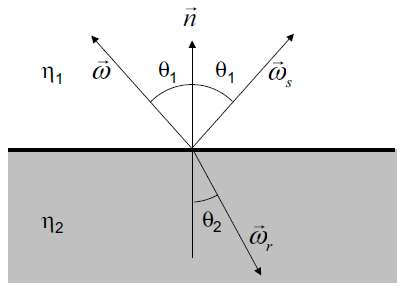 Vyrátať chceme smer lúča omega r. Ostatné veličiny z obrázku sú nám známe. Po dlhom odvodení dostaneme nasledovný vzorec pre lúč omega r:
Vyrátať chceme smer lúča omega r. Ostatné veličiny z obrázku sú nám známe. Po dlhom odvodení dostaneme nasledovný vzorec pre lúč omega r:
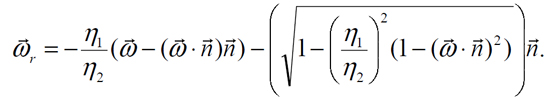
Komentáre
Musíte byť prihlásenýpre komentovanie.