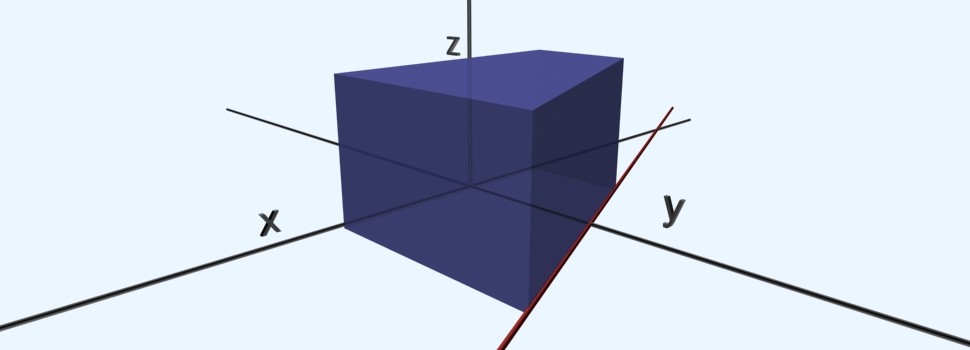
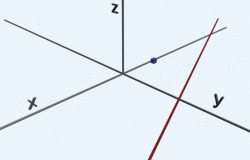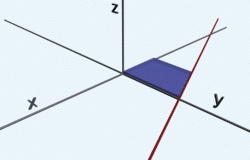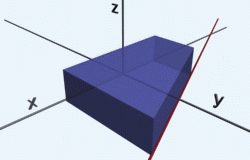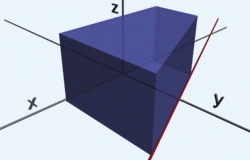
Objem telies (miera trojdimenzionálnej množiny) sa počíta pomocou trojných integrálov. Avšak ako všetci vieme zo základnej školy, tak napríklad objem kocky vieme vyrátať ako dĺžku strany na tretiu, objem kvádra ako súčin troch dĺžok jeho strán, objem guľe ako 4/3*pí*r^3 a podobné známe vzorce. Všetky tieto vzorce sú všeobecne odvodené z ešte všeobecnejšieho výpočtu objemu a to práve pomocou trojných integrálov. Ukážme si to na jednoduchom príklade, výpočet objemu kvádra s dĺžkami strán a=4, b=2,c=8, ktorý je umiestnený v strede súradnicovej sústavy:

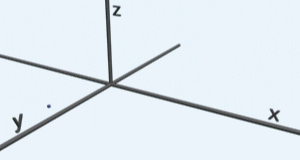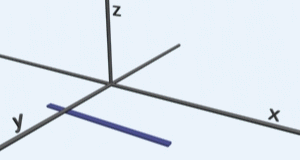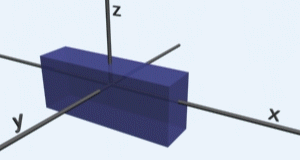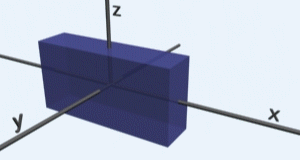
Ako môžete vidieť názorne na animovanom obrázku, teleso sa trojitým integrovaním akoby vytvára, najprv v smere x od -4 po 4, potom v smere y od -1 po 1 a následne v smere z od -2 po 2. Integrujeme jednotku. Tento príklad je veľmi jednoduchým príkladom, kde žiadna dĺžka (ohraničenie) nezávisí od inej. Pri výpočte to vidíme na tvaroch funkcií po zintegrovaní podľa každej premennej, kde nám vždy ostala práve iba daná premenná. To znamená, že ak napríklad do funcie f(x)=x dosadzujeme čísla, vždy dostávame naspať práve to číslo.

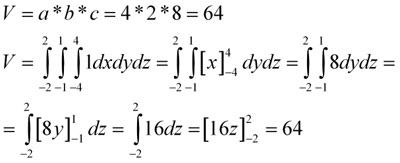To nám obrázkovo hovorí, že objem sa bude vytvárať akýmsi “ťahaním” hmoty, ako vidíme na animácii hore. Počas ťahania v každom smere sa už šírka nijako nemení. Avšak tak ako pri plochách, tak aj pri objemoch môže opačný prípad nastať. Najprv sa však pozrime na odvodenie vzorca pre výpočet objemu guľe, ktorý je zaujímavý najmä preto, lebo na strednej škole sme ho dostali pevne daný a nikto vám nepovedal, prečo je to tak.

Odvodenie vzorca pre objem gule

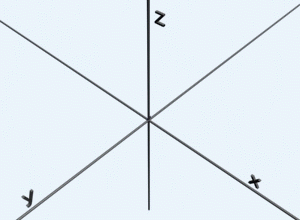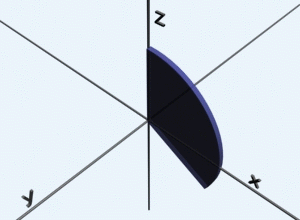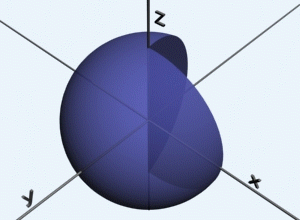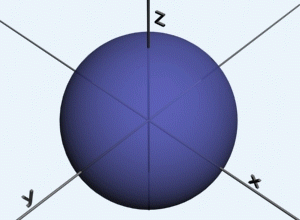
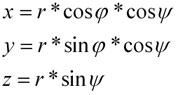Keďže ide o guľové teleso, zaveďme si sférické súradnice (hore). Pri transformácií však nesmieme zabudnúť na Jakobián. Pri trojnom integrovaní budeme teda integrovať súčin jednotky a Jakobiánu, teda iba samotný Jakobián. Zo strednej školy poznáme pre výpočet objemu guľe vzorec 4/3*pí*r^3, kde r predstavuje polomer gule. Ako uvidíme, práve k tomuto vzorcu sa dopracujeme. Tak ako v predchádzajúcom prípade, objem sa integrovaním akoby vytvorí. Stačí si určiť vhodné hranice integrovania. Podľa r, polomeru, budeme integrovať od 0 po r, čo vlastne predstavuje vnútro našej guľe. Podľa psí od -pí/2 po pí/2 a podľa fí od 0 po pí. Názornejšie to uvidíme na animovanom obrázku. Trojný integrál stačí vypočítať a ako vidno, dostali sme presne náš vzorec.

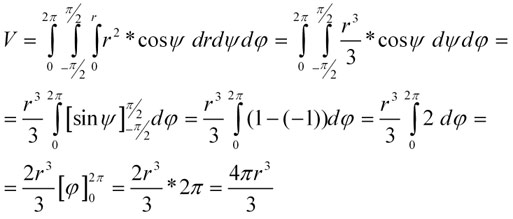
Poznámka: Po transformácií súradníc už neplatí pravidlo ťahania objemu podľa vzniknutej funkcie, ako v prvom príklade.
Na podobnom princípe, tj postupné vytváranie objemu pomocou integrovania, budú fungovať všetky príklady, ktoré si vysvetlíme. Samozrejme budú o čosi zložitejšie.

Zrezaný kváder

Prvým problémom môže byť poradie integrovania. V predošlých dvoch príkladoch na poradí nezáležalo, keďže žiaden rozmer nebol závislý na inom, tj. všetky premenné boli nezávislé. Opačným príkladom môže byť napríklad akýsi zrezaný kváder, ktorý v smere y je závislý na x, navyše y>0, -2>x>3 a v smere z je kváder natiahnutý od 0 po 3, všetko vidno na obrázkoch. Pre správnosť uvádzame aj matematicky zapísané zadanie telesa.

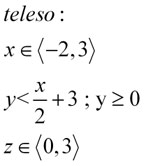
Na prvom obrázku vidíme situáciu v rovine xy, kde je červeným vyznačená daná funkcia a modrým daná plocha od nuly až po fukciu.

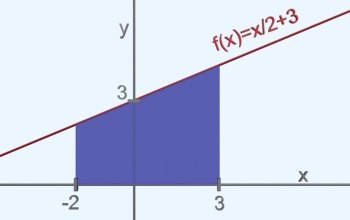
A tu vidíme situáciu už v priestore xyz, zrezaný kváder.

Pri tomto výpočte nepoužijeme žiadnu transformáciu súradníc, čiže integrovať budeme jednotku.

Pri výpočte objemu klasického kvádra hore sme po zintegrovaní dostali vždy práve jednu premennú. Avšak ak sa pozrieme na výpočet tohto trojného integrálu, kde hranica y je závislá od x, zistíme, že po zintegrovaní podľa y dostaneme funkciu závislú od x a po jej zintegrovaní podľa x nedostaneme iba jednoduchú f(x)=x (ako v príklade hore), ale bude to f(x)=x^2/4+3x. To laicky povedané znamená, že po dosadení nejakého čísla do funkcie dostaneme naspäť iné číslo. Z toho sa dá obrázkovo povedať, že objem sa v smere x nebude vytvárať “ťahaním” konštantnej hmoty, ale meniacej sa hmoty, tj počas ťahania mení svoju šírku. Vidieť to aj na animácii. Preto je dôležité zvoliť správne poradie integrovania, pretože ak by sme integrovali najprv podľa x a potom podľa y, tak po prvom zintegrovaní podľa x dostaneme funkciu f(x)=x, čiže hmotu by sme v smere x mali ťahať s nemeniacou sa šírkou, to však nesedí. Navyše ak potom zintegrujeme podľa y, opäť sa nám tam objaví x. To znamená, že v konečnom výsledku by nám x ostalo, takže by sme vôbec nedostali konkrétny výsledok. Pre ilustráciu uvádzame obidva výpočty a taktiež animáciu obidvoch výpočtov.

Správne riešenie:

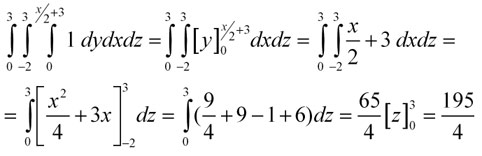
Nesprávne riešenie:

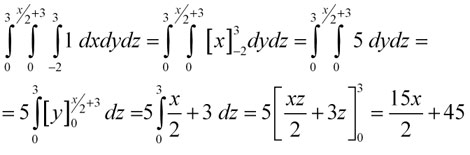
Článok a animácie pre vás pripravil Stanislav Griguš v roku 2011, ale platí to aj dnes,.. tak učte sa! :P